基礎理論　予想問題

問題　28問　公開

NO	解答 解説	問題
1	解答解説	16進数のA9＋B5の結果として正しいものはどれか。(N進数XをXnと表現します) ア　101010112　イ　4368　ウ　5168　エ　5368
2	解答解説	2進数の1.1011と1.1101を加算した結果を10進数で表したものはどれか。 ア　3.1　イ　3.375　ウ　3.5　エ　3.8
3	解答解説	10進数の125を3進数へ変換した場合の桁数はいくつになるか。 ア　3　イ　4　ウ　5　エ　6
4	解答解説	10進数の0.40625を2進数で表したものはどれか。 ア　0.01001　イ　0.0101　ウ　0.01011　エ　0.01101
5	解答解説	アルファベットのAを10進数の0、Bを1、Cを2・・・Zを25とする26進数がある。このとき、次の計算式は幾らになるか。 DOG＋CAT－FOX ア　A　イ　B　ウ C　エ　D
6	解答解説	10進数の-100を2の補数表現で8ビットのレジスタへ記憶する。これを右に3ビット算術シフトした結果を10進数で表したものはどれか ア　-33　イ　-13　ウ　-12　エ　19
7	解答解説	2進数00010111を左へ3ビツト論理シフトしたものと01010101を右へ3ビット論理シフトしたものの排他的論理和を16進数で表したものはどれか。(論理シフトではシフト後の空きビットには0が入ります) ア B2　　イ C3　　ウ F2　　エ B1
8	解答解説	4ビツトの情報x1x2x3x4に対して、 (x1+x2+x3+x5) mod 2 = 0 (x1+x2+x4+x6) mod 2 = 0 (x2+x3+x4+x7) mod 2 = 0 を満たす冗長ビツトx5x6x7を付加した符号x1x2x3x4x5x6x7を送信する。1ビットの誤りを含むビット列1100010を受信した時、正しい情報ビットはどれか。 (a mod bは、aをbで割った余りを表す) ア　0100　イ　1000　ウ　1100　エ　1101
9	解答解説	10進数-5.625を、8ビット固定小数点形式による2進数で表したものはどれか。負数には2の補数表現を用いる。(小数点位置は、4ビット目と5ビット目の間とする) 8 7 6 5 4 3 2 1 　　 　　 　　 　　 　　 　　 　　 　　 　 ▲ 　 ア　01001100　イ　10100101　ウ　10100110　エ　11010011
10	解答解説	正規化した2進浮動小数点を、符号が1ビット、指数部が8ビット、仮数部が23ビツトで表現した。これを10進数に変換すると、有効な桁数はどれだけか。 (必要ならば、log102=0.301を使用しても良い) ア 6　イ　7　ウ　8　エ　10
11	解答解説	有効桁数4桁で、次の10進浮動小数点演算を行うとき、発生する誤差に関する記述のうち、正しいものはどれか。ここで、計算は加算、減算の順に行うものとする。 「計算式」　1234＋1.987－1233 ア　加算、減算ともにけた落ちが生じる イ　加算、減算ともに情報落ちが生じる ウ　加算でけた落ちが、減算で情報落ちが生じる エ　加算で情報落ちが、減算でけた落ちが生じる
12	解答解説	100人の学生で、スペイン語を学んでいるのは18人、ドイツ語は40人、フランス語は42人であった。また、スペイン語とドイツ語は6人、ドイツ語とフランス語は15人、フランス語とスペイン語は5人、3言語すべては2人であった。いずれの語学も学んでいない学生は何人か。 ア　22　イ　24　ウ　26　エ　28
13	解答解説	XとYの否定論理積 X NAND Y は、NOT(X AND Y)として定義される。 X OR Y をNANDだけを使って表した論理式はどれか。 ア　((X NAND Y) NAND X) NAND Y イ　(X NAND X) NAND (Y NAND Y) ウ　(X NAND Y) NAND (X NAND Y) エ　X NAND (Y NAND (X NAND Y))
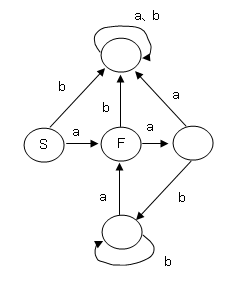
14	解答解説	次の有限オートマンで受理されるものはどれか。ただし、a、bは入力アルファベット、Sは開始状態、Fは受理状態とする。 ア　aaba　イ　abaab　ウ baabb　エ　abbba
15	解答解説	正規表現 [A-Z]＋[0-9]* が表現する文字列の集合の要素となるものはどれか。 ここで、 [A-Z]：英字1文字を表す。 [0-9]：数字1文字を表す。 * は、直前の正規表現の0回以上の繰返しを表す。 + は、直前の正規表現の1回以上の繰返しを表す。 ア　456789　イ　ABC99*　ウ　ABC+99　エ　ABCDEF
16	解答解説	次に示すのは、BNFで記述されたあるプログラム言語の構文の一部である。 <パラメタ指定>として、正しいのはどれか。 <パラメタ指定>：：=<パラメタ>|(<パラメタ指定>、<パラメタ>) <パラメタ>：：=<英字>|<パラメタ><英字> <英字>：：=a|b|c|・・・|x|y|z ア　((abc、def))　イ　((abc、def)、ghi)　ウ　(abc)　エ　(abc、(def))
17	解答解説	次の式を逆ポーランド表記法で表現したものはどれか。 (A+B)×(C+D) ------------ 　　　A-D ア A+B×C+D÷A-D イ AB+CD+×AD-÷ ウ ABCD++×AD-÷ 5 エ ABCD++÷AD-×
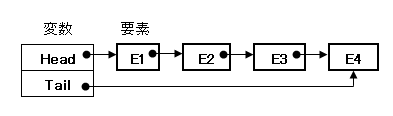
18	解答解説	次のような構造をもった線形リストに関する記述のうち、正しいものはどれか。 ア　要素の削除に要する処理量は、先頭と最後尾とでほぼ同じである。 イ　要素の追加と取出し(読出しの後で削除)を最後尾で行うスタックとして用いるのに適している。 ウ　要素の追加に要する処理量は、先頭と最後尾とでほぼ同じである。 エ　要素の追加は先頭で、取出し(読出しの後で削除)は最後尾で行うFIFOのキューとして用いるのに適している。
19	解答解説	A、B、Cの順番で入力されるデータがある。各データについてスタックへの挿入と取出しを一度ずつ任意のタイミングで可能とする場合、データの出力順序は何通りあるか。 ア　3　イ　4　ウ　5　エ　6
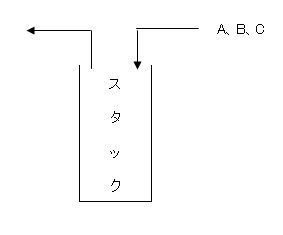
20	解答解説	スタックとキューの二つのデータ構造がある。次の手続を順に実行した場合、変数xに代入されるデータはどれか。 ここで、 データaをスタックに挿入することを、push(a) スタックからデータを取り出すことを、pop() データaをキューに挿入することを、enq(a) キューからデータを取り出すことを、deq() とそれぞれ表す。 push(a) push(b) enq(pop()) enq(c) push(d) push(deq()) x=pop() ア　a　イ　b　ウ　c　エ　d
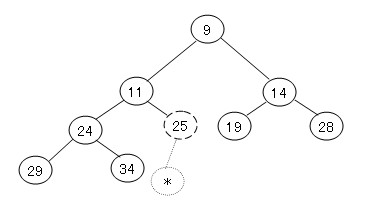
21	解答解説	以下のような関係を持ったヒープがある。このヒープの要素25の下(*)へ要素7を追加したとき、要素25の位置にくる要素はどれか。 ア　7　イ　9　ウ　11　エ　24
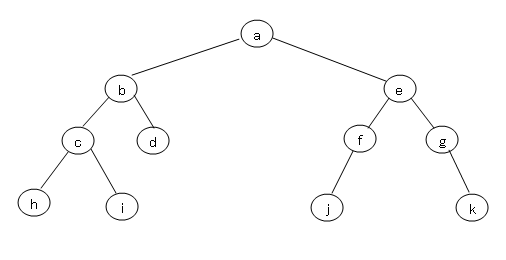
22	解答解説	下図は2分木です。この2分木で、走査を以下のように行った場合、節の値を出力した結果はどれか。 左部分木、右部分木、節点の順に走査する(後順走査) ア　abchidefjgk　イ abechidfjgk　ウ hcibdajfegk　エ hicdbjfkgea
23	解答解説	下図の10件をキーとするレコードをファイルへ記録する時、ハッシング(アドレス変換)の方法として、5を除数とする除算法を用いたとき、シノニムレコードは何件か。 (除算法は、5で割った余りをハッシュ値とする) 2 3 4 9 11 13 15 18 20 23 ア　1　イ　2　ウ　3　エ　4
24	解答解説	あらかじめ整列された1000人分の電話番号を2分検索法を用いて検索するとき、最大何回の比較で見つかるか。 ア　7　イ　8　ウ　9　エ　10
25	解答解説	99個の異なるデータを格納したテーブルを線形検索する場合、平均何回の比較で目的のデータを探すことができるか。ここで、目的のデータがテーブル中に存在しない確率を10％とする。 ア　45　イ　49.5　ウ　54.45　エ　54.9
26	解答解説	次の6個の要素をもつ配列を、右から左へのパブルソートのアルゴリズムによって昇順に整列するとき、3回目のスキャン後の配列はどれか。 整列前の配列：10　8　52　17　3　31 ア　3　8　10　17　31　52 イ　3　8　10　17　52　31 ウ　3　8　52　17　10　31 エ　3　10　8　52　17　31
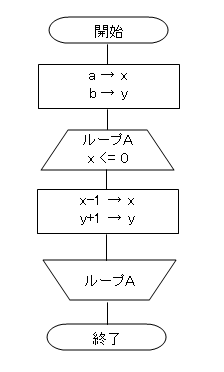
27	解答解説	a、bを整数とする、次の流れ図によって表されるアルゴリズムを実行した後、、a、bの値に無関係に成り立つ条件はどれか。 ア　x=0かつy=a+b　イ　x=aかつy=b　ウx+y=a+b　エ　x-a=y-b
28	解答解説	非負の整数nに対して次のように定義された関数F(n)、G(n)がある。F(5)の値は幾らか。 F(n)：If n <= 1 then 1 else n×G(n-1) G(n)：If n = 0 then 0 else n + F(n-1) ア　50　イ　65　ウ　100　エ　120

解答・解説

NO	解答	問題へ	解説
1	エ	問題へ	この問題の手順は、まず10進数に変換して、加算を行い、8進数と2進数へ変換するという手順を踏む必要があります。 A916=10×161＋9×160=10×16＋9×1=16910 B516=11×161＋5×160=11×16＋5×1=18110 上記を加算して、169＋181=35010 35010を8進数へ変換して見ます。 8 350 　 8 43 6 　 5 3 これより、5368となります。
2	ウ	問題へ	まず、2進数の加算を行います。 　 1.1011 ＋ 1.1101 答 11.1000 ここで、整数部は、(11)2=(3)10となります。小数部は、(0.1)ですから10進数に変換すると、1×2-1=1/21=(0.5)10となります。よって、(3.5)10となります。
3	ウ	問題へ	これは、3進数へ変換するため、3で割り算を行い、余りの桁数を求めます。 3 125 余り 3 41 2 3 13 2 3 4 1 　 1 1 111223となり、桁数は、5桁となります。
4	エ	問題へ	小数の10進数から2進数の変換方法は、2で乗算を行い、整数部を取り出して行きます。 0.40625×2=0.8125 0.8125×2=1.625 0.625×2=1.25 0.25×2=0.5 0.5×2=1.0 上記に0.を付けて太字の部分を順番に並べます。0.01101となります。
5	ウ	問題へ	問題の仕様は26進数ですから、DOG＋CAT－FOXを10進数に変換して計算を行います。 DOG=D×262＋O×261＋G×260=3×676＋14×26＋6=2398 同様にして、 CAT=1371 FOX=3767 となります。 よって、DOG＋CAT－FOX=2398＋1371－3767=2 ここで得られた「2」は10進数です。よって26進数では「C」となります。
6	イ	問題へ	まず、100を2進数で表現して2の補数へ変換します。 10010=011001002となり、これの2の補数を求めます。(ビットを反転させて+1する) 01100100 10011011 +1する 10011100 次に算術シフトを行います。これは、一番左側を符号ビットとして、これは動かさず、残りの部分をシフトします。空いた部分には「1」を埋めます。よって、 11110011　(右側の100は捨てられます)。これがシフト結果となります。 次に、10進数で、これの値を求めます。これは、2の補数の求め方の逆を行います。 つまり、-1してビットを反転させます。 11110011 -1 11110010 00001101 =(13)10 求めているのは負数のため、-13となります。
7	ア	問題へ	2進数00010111を左へ3ビット論理シフトすると、 10111000となります。 2進数01010101を右へ3ビット論理シフトすると、 00001010となります。 両者の排他的論理和(※ビットが同じ場合は「0」となります)を求めます。 10111000 00001010 排他的論理和は、 10110010となります。 これを16進数へ変換する場合は、4ビットずつ区切って16進数で表現します。 1011 11で、B 0010 2で、2 よって、B2となります。
8	エ	問題へ	受信したビット列(1100010)をxで表現すると、 x1=1 x2=1 x3=0 x4=0 x5=0 x6=1 x7=0　となります。 これを式にあてはめます。 (1+1+0+0) mod 2 = 0 (1+1+0+1) mod 2 = 1 (1+0+0+0) mod 2 = 1 仮に、誤りがない場合は、上記の3つ式は、すべて0となります。 2・3番目が0でないため、2・3番目の式に共通して1番目の式に含まれないものが誤りのビットとなります。よってx4となります。従って、x1=1 x2=1 x3=0 x4=0で、x4を1にすればよいことになります。よって、1100->1101となります。
9	ウ	問題へ	まず、-5.625の絶対値を2進数へ変換します。 5=101 0.625=0.101　となり、それぞれ4ビットで表現すると、01011010となります。 これに2の補数を求めます。ビットを反転させて+1します。 01011010 10100101 +1 10100110　となります。
10	ア	問題へ	浮動小数点形式の有効桁数は、仮数部の長さで決定します。これが2進数で23ビットですから、10進数に変換した時の有効桁数をxとすると、 223=10x が成立します。これより、対数を使用して、 x=log10223 と変換できます。 x=23log102 = 23×0.301 = 6.923 で切り捨てて、6桁となります。
11	エ	問題へ	まず、加算・減算の順に計算を行うわけですから、 (加算) 1234＋1.987=1235となります。(有効桁数が4桁のため小数部が切り捨てられる。これは情報落ちが発生しています。) (減算) 1235-1233=2となります。(有効桁数が4桁から1桁になったため、けた落ちが発生しています)
12	イ	問題へ	ベン図を書くとわかりやすいかと思いますが、問題文より計算してみると、 (1)スペイン語とドイツ語だけ=6-2=4人 (2)ドイツ語とフランス語だけ=15-2=13人 (3)フランス語とスペイン語だけ=5-2=3人 これより、 (4)スペイン語だけ=18-(4+3+2)=9人 (5)ドイツ語だけ=40-(4+13+2)=21人 (6)フランス語だけ=42-(13+3+2)=24人 よって、解答は、 100-(9+21+24+4+13+3+2)=100-76=24人
13	イ	問題へ
14	ア	問題へ	Sが始まりで、最後がFであるものを選択すれば良いわけです。 アのaabaは、S->F->右の○->下の○->Fとなり、受理されたことになります。他の選択肢では、最後がFになりません。
15	エ	問題へ	[A-Z]+ は、英字の1文字以上の並びを表現しています。 [0-9]* は、数字の0文字以上の並びを表現しています。 従って、英字のみのエが正解となります。
16	イ	問題へ	パラメタ指定の定義より、パラメタのみか、または、パラメタ指定、パラメタのいずれかである。よって、イについては、((abc、def)、ghi)は、abcはパラメタで、defもパラメタです。これを(abc、def)とした場合(パラメタ、パラメタ)でパラメータ指定です。 また、これより、((abc、def)、ghi)は、(パラメータ指定、ghi)で、(パラメータ指定、パラメタ)でパラメタ指定となります。 不正解の理由は以下の通りです。 ●アについて (abc,ghi)ならば、パラメータ指定であるが外側のカッコを加えるとパラメータが1個となるため不正解となります。 ●ウについて (abc)はパラメータであるが、パラメータ指定では、「,」が必要であるため、不正解となります。 ●エについて (abc、(def))で、最初のabcはパラメタです。しかし次の「,」の後の(def)はパラメタが1個しかないため、パラメタ指定の記法に合致していないため不正解となります。
17	イ	問題へ	(A+B)は、AB+となり、(C+D)は、CD+となります。これを乗算しているので、AB+CD+×となります。次に、(A-D)は、AD-となり、分子÷分母のため、AB+CD+×AD-÷となります。
18	ウ	問題へ	線形リストの各要素は「データ部分」と「次の要素のアドレス」を格納しています。変数の「Head」は先頭の要素のアドレスを記憶して、「Tail」は最後尾の要素のアドレスを格納しています。ここで先頭要素へ追加する場合は、Headを変更して、新しい要素のアドレスをE1をさすようにします。最後尾に追加する場合は、変数Tailのアドレスを変更して、E4が最後の要素のアドレスを指すように変更します。つまり、どちらも、処理量は同様です。
19	ウ	問題へ	スタックとは、LIFOの後入れ先出しのデータ構造です。つまり、一番最後に挿入されたデータが最初に取り出されます。 ●Aを挿入して他のデータを挿入する前にAを取り出す場合。 　A-B-CとA-C-B ●Aを挿入後、他のデータの挿入・取り出しを行い、最後にAを取り出す場合。 　B-C-AとC-B-A ●A、Bを挿入後、これらを取り出してから、Cを挿入して取り出す場合。 　B-A-C 出力順序は以上の5種類となります。
20	イ	問題へ	スタックは、LIFO(後入れ先出し)で、キューはFIFO(先入れ先出し)のデータ構造です。 ●push(a)で、aをスタックへ挿入 ●push(b)で、bをスタックへ挿入 ●enq(pop())で、スタックからデータを取り出し(b)、それをキューへ挿入(b) ●enq(c)で、データcをキューへ挿入 ●push(d)で、データdをスタックへ挿入 ●push(deq())で、キューからデータを取り出し(b)、それをスタックへ挿入(b) ●x=pop()で、スタックからデータを取り出す。これは、上記よりbが最後に挿入されたデータであるため、bが取り出されます。
21	ウ	問題へ	ヒープで、親の値<=子の値の関係を持ったものです。25の要素の下へ要素7を追加した場合、 ●25と7を入れ替える。 ●7と11を入れ替える。 ●7と9を入れ替える。 よって25の要素のところには、11の要素が配置されます。
22	エ	問題へ	問題文より、左部分木、右部分木、節点の順に走査する(後順走査)とあるので、hについては、左２分木・右2分木もないので、ここが出発点となります。後は同じレベルのものを左から右へ行き、次に上へ行くという順序となります。
23	ウ	問題へ	実際にキー値より5で除算を行い余りをハッシュ値として計算を行います。 キー値 2 3 4 9 11 13 15 18 20 23 ハッシュ値 2 3 4 4 1 3 0 3 0 3 よってシノニム(ハッシュ値が複数あるもの)は、0、3、4の3件のレコードとなります。
24	エ	問題へ	2分検索法で要素数が、Nの時、以下の関係が成立します。 2m <= N < 2(m+1)　(mは平均比較回数、m+1は最大比較回数) これより、1000個の要素では、 29 <= 1000 < 210　となります。 よって、10となります。
25	エ	問題へ	N個のデータの線形検索法の比較平均値は、(1＋N)÷2となり、 これより、(1＋99)÷2=50となります。 上記は、必ず見つかる場合です。見つからない場合の比較回数は、すべて比較するため、99回となります。確率10％より、以下の通りとなります。 99×0.1＋50×0.9=54.9
26	ア	問題へ	バブルソートは交換法とも言います。これは、端から隣り合う要素を比較して、大小が逆であれば交換を行うという方法です。この場合は、右から比較していきます。 1回目のスキャンでは、 3が一番左に移動されます。 3　１０　8　52　17　31となります　 2回目のスキャンでは、 17と52を交換して、8と10を交換します。 3　８　10　17　52　31 3回目のスキャンでは、 31と52を交換します。 3　8　10　17　31　52 よってアとなります。
27	ウ	問題へ	この流れ図は、初期値として、xとyをセツトして、xが0以下になるまで、ループ処理を行い、その中で、xは-1ずつ減算して、yは+1ずつ加算しています。 例えば、a=10 b=15の時、この処理を実行すると、xとyの初期値はa bと等しいところからループ処理を行います。この中で、 xは、 9 8 7 6 5 4 3 2 1 0 yは、16 17 18 19 20 21 22 23 24 25 と変化していきます。(ここで、x+y=25が成立しています) a bは変化しないため、a+b=25です。 また、x+y=25となります。 よって、x+y=a+bという関係が成立します。
28	イ	問題へ	再帰に関する問題です。求めるのは、F(5)ですから、F(1)より求めていきます。但し、G関数が必要なため、具体的には交互に求めていきます。 F(1)=1 G(2)=2+F(1)=2+1=3 F(3)=3×G(2)=3×3=9 G(4)=4+F(3)=4+9=13 F(5)=5×G(4)=5×13=65

pafuイーランスクール